An Equilateral Triangle Inscribed Inside A Given Circle

You are going to learn how to inscribe an equilateral triangle inside a given circle, using only a pencil, a straight edge and a pair of compasses. The side length of the inscribed equilateral triangle will also be determined.

Use the pencil and the pair of compasses to draw the circle. Label the centre point of the circle ‘O’; it will be highlighted in the drawings by a small black disc. Choose an arbitrary point on the circumference of the circle; this point will become one of the vertices of the equilateral triangle. Label the selected point ‘A’; it will be highlighted in the drawings by a small red disc. See Figure 1.

Figure 1.

Now place the point of the pair of compasses on ‘A’ and lightly draw a small arc above it that intersects with the circumference of the circle, thus:

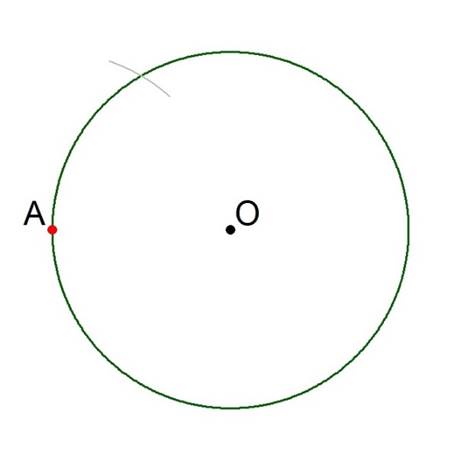
Figure 2.

Label the point at which this arc intersects the circumference of the circle ‘P’; it will be highlighted in the drawings by a small black disc. See Figure 3.

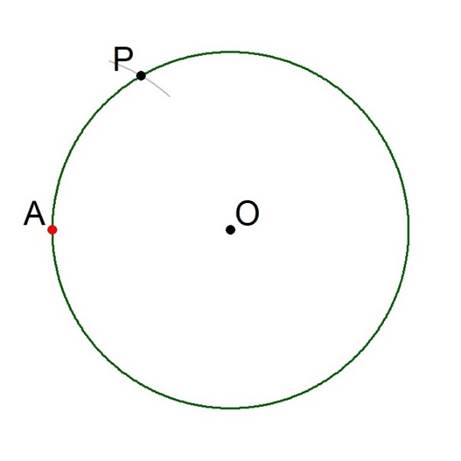
Figure 3.

We shall now pause the construction for a moment to establish a result that will be used to justify the validity of our construction.

Consider the triangle formed by the three points A, O and P:

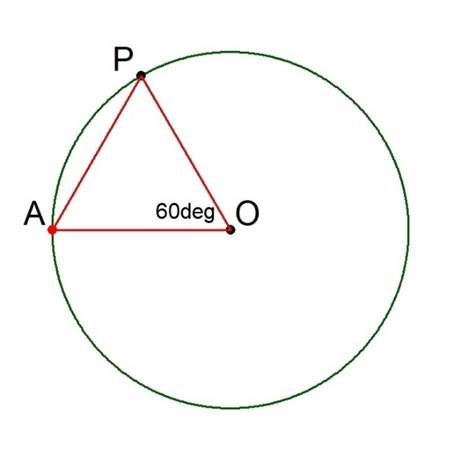
Figure 4.

The sides OA and OP are radii of the circle, and by construction the length of AP is also the radius. Thus, triangle AOP is equilateral (“equal sides”). Euclid’s Proposition I.8 asserts that it is also equiangular (“equal angles”), and, since the angles of any triangle sum to 180° (Euclid’s Proposition I.32), each angle must be 60°. In particular, note that the angle AOP is 60°.

The angle AOP is also the “angle subtended at the centre by the arc AP”, as shown in Figure 5.

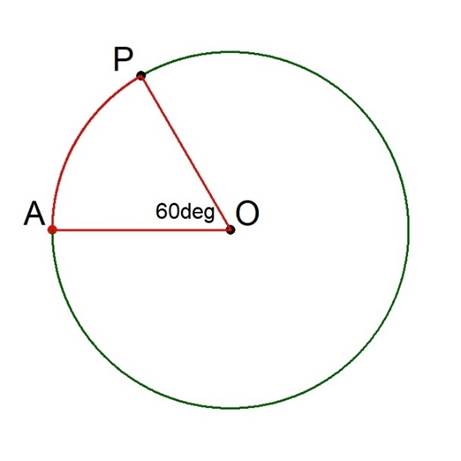
Figure 5.

Thus, the constructive step that led to finding the point P formed an arc AP that subtends an angle of 60° at the centre of the circle. The circle is 360°, and so five further iterations of the constructive step, each time moving the point of the compasses onto the point found in the previous step, will bring you exactly back to the original point A. See Figure 6.

Figure 6.

Take every second iteration and label the point of intersection with the circumference of the circle ‘B’ and ‘C’, respectively; they will be highlighted in the drawings by small red discs. See Figure 7.

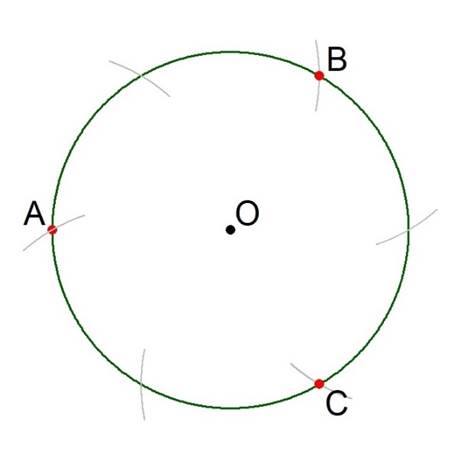
Figure 7.

Use the straight edge to form the triangle ABC. See Figure 8.

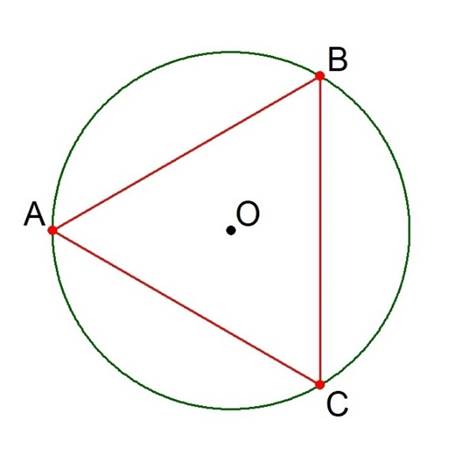
Figure 8.

The triangle ABC is inscribed in the circle, and by the symmetry of our construction is equilateral.

What is the side-length of the inscribed equilateral triangle?

Let us return to the constructive phase as exemplified in Figure 5. Having started at A, the second and fourth iterations of the constructive steps gave the points B and C. Now let us identify the third iteration and label the point of intersection with the circumference of the circle ‘Q’; it will be highlighted in the drawings by a small black disc. See Figure 9.

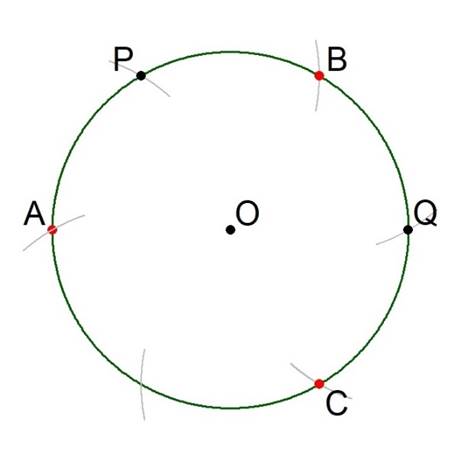
Figure 9.

Recall that it was established (see Figure 5) that each iteration of the constructive step created a new arc on the circumference of the circle which subtended an angle of 60° at the centre of the circle. Thus, the three iterations needed to get the point Q forms an arc APBQ that subtends an angle of 3 × 60° = 180° at the centre of the circle. See Figure 10.

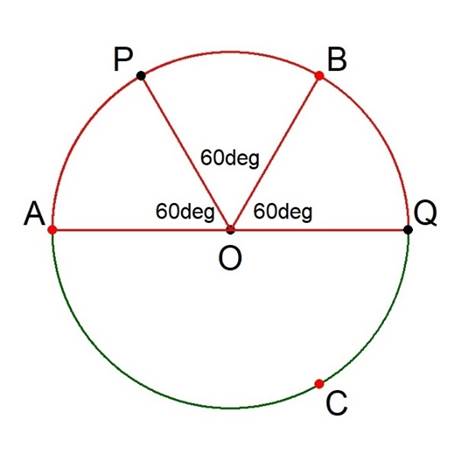
Figure 10.

But, if the angle AOQ is 180°, then AOQ is a straight-line segment, and AQ is a diameter of the circle. The length of AQ, ǁAQǁ, is twice the radius of the circle.

BQ is a straight-line segment, which by construction has the length of the radius of the circle.

So, focussing on the triangle formed by the points A, B and Q, we have Figure 11.

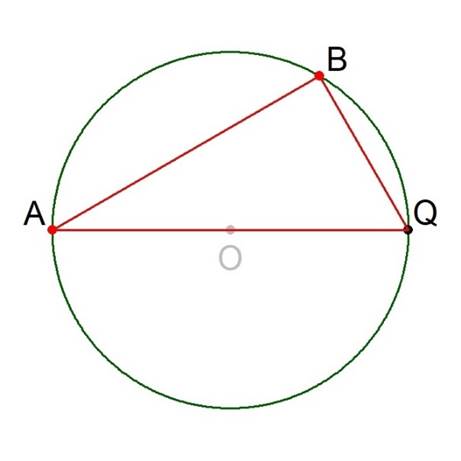
Figure 11.

The side-length ǁABǁ is the quantity whose value we seek.

The side-length ǁBQǁ is the radius.

The side-length ǁQAǁ is twice the radius.

But how do these relate to each other?

Euclid’s Proposition III.31 asserts that the angle at the circumference of a circle subtended by a diameter of the circle is a right angle, 90°. Thus, the angle ABQ is a right angle.

Euclid’s Proposition I.47, more familiarly known as Pythagoras’ Theorem, now comes into play, and asserts that

ǁQAǁ² = ǁABǁ² + ǁBQǁ²

Solving for ǁABǁ gives that the side-length of the inscribed equilateral triangle is

(√3) × (radius)